Last week, I unveiled my NBA Adjusted Efficiency rating system. This week, I’ll explore some of the decisions I made with that system, per the request of Ben.
The first question is how much the ranking are effected by using rest-days adjustments. See my original research on APBRmetrics for where this comes from. Here’s a table comparing the effect on each team:
| Team | Rest-Adjusted | Not Rest-Adjusted | Difference |
|---|---|---|---|
| ATL | 2.88 | 2.46 | 0.42 |
| BOS | 7.99 | 7.32 | 0.67 |
| CHA | -3.72 | -3.59 | -0.13 |
| CHI | 4.63 | 4.16 | 0.47 |
| CLE | -10.81 | -10.85 | 0.04 |
| DAL | 4.17 | 4.58 | -0.41 |
| DEN | 2.55 | 2.39 | 0.16 |
| DET | -5.83 | -5.55 | -0.28 |
| GSW | -2.77 | -2.75 | -0.02 |
| HOU | -0.11 | 0.07 | -0.18 |
| IND | -1.42 | -1.31 | -0.11 |
| LAC | -2.96 | -3.56 | 0.61 |
| LAL | 7.13 | 6.34 | 0.79 |
| MEM | 1.26 | 0.64 | 0.63 |
| MIA | 8.33 | 8.55 | -0.22 |
| MIL | -1.49 | -1.39 | -0.10 |
| MIN | -4.71 | -4.55 | -0.16 |
| NJN | -6.38 | -6.54 | 0.16 |
| NOH | 2.27 | 2.96 | -0.70 |
| NYK | 2.22 | 2.12 | 0.10 |
| OKC | 2.48 | 2.95 | -0.46 |
| ORL | 4.84 | 4.98 | -0.14 |
| PHI | 0.36 | 0.10 | 0.26 |
| PHO | -2.33 | -2.33 | 0.00 |
| POR | 1.40 | 1.74 | -0.34 |
| SAC | -8.79 | -8.48 | -0.31 |
| SAS | 7.40 | 8.01 | -0.61 |
| TOR | -4.78 | -4.77 | -0.01 |
| UTA | 3.26 | 3.05 | 0.21 |
| WAS | -7.09 | -6.76 | -0.33 |
The average difference is 0.30. As the season goes on, the difference should decrease as the rest situations equalize over time. Over the whole year, though, there are certainly still advantages and disadvantages based on scheduling. I haven’t tabulated them based on my updated estimate of rest day impact, but earlier, with older estimates, I used rest-days adjustments in my prediction of wins for this season.
Question 2 is based on my choice of 1.5 as the exponent of residuals to minimize. EDIT: (That’s formulated (abs(residual))^1.5, Ryan.) A true arithmetic mean is effectively minimizing residuals^2. I chose 1.5. Why? Well, just gut feeling mostly, but I will eventually investigate what exponent is the best. The question, though, is best for what? What is the objective? With residuals^2, outliers like the Lakers’ pounding of Cleveland 112 to 57 have a huge effect. On the other hand, minimizing residuals alone under-weights the outliers–in fact, minimizing pure residuals gives you the median of the set! Here’s an example:
Take a distribution of 5 numbers: -2, -1, 0, 3, 11. What is the result of minimizing residuals, residuals^1.5, or residuals^2? Let’s throw this in Excel and look at the results
| Exponent: | 1 | 1.25 | 1.5 | 1.75 | 2 | 2.25 | 2.5 |
|---|---|---|---|---|---|---|---|
| Cald'd Mean | 0.00 | 0.35 | 1.27 | 1.80 | 2.20 | 2.55 | 2.87 |
| Value | Err | ||||||
| -2 | 2.0 | 2.9 | 5.9 | 10.3 | 17.6 | 30.3 | 52.3 |
| -1 | 1.0 | 1.5 | 3.4 | 6.0 | 10.2 | 17.3 | 29.5 |
| 0 | 0.0 | 0.3 | 1.4 | 2.8 | 4.8 | 8.2 | 14.0 |
| 3 | 3.0 | 3.4 | 2.3 | 1.4 | 0.6 | 0.2 | 0.0 |
| 11 | 11.0 | 19.2 | 30.4 | 48.6 | 77.4 | 121.6 | 188.4 |
| Sum Error | 17.0 | 27.3 | 43.4 | 69.2 | 110.8 | 177.7 | 284.2 |
| Mean | 2.20 | ||||||
| Median | 0 |
Minimizing residuals^1.5 yields a result in between the mean and the median, obviously. I’ll revisit this another time… but first, a table comparing the ratings using residuals, residuals^1.5, and residuals^2 to get the results:
| Team | Residuals^1 | Residuals^1.5 | Residuals^2 | Skew |
|---|---|---|---|---|
| MIA | 8.02 | 8.33 | 8.36 | 0.34 |
| BOS | 8.15 | 7.99 | 7.99 | -0.16 |
| SAS | 7.69 | 7.40 | 7.23 | -0.46 |
| LAL | 7.23 | 7.13 | 7.01 | -0.22 |
| ORL | 4.86 | 4.84 | 5.11 | 0.25 |
| CHI | 4.17 | 4.63 | 4.95 | 0.78 |
| DAL | 4.93 | 4.17 | 4.06 | -0.87 |
| UTA | 5.68 | 3.26 | 2.35 | -3.33 |
| ATL | 2.01 | 2.88 | 2.84 | 0.83 |
| DEN | 1.31 | 2.55 | 3.21 | 1.90 |
| OKC | 2.82 | 2.48 | 1.74 | -1.08 |
| NOH | 2.87 | 2.27 | 2.17 | -0.70 |
| NYK | 2.57 | 2.22 | 1.86 | -0.71 |
| POR | 1.39 | 1.40 | 1.34 | -0.05 |
| MEM | 1.17 | 1.26 | 0.90 | -0.27 |
| PHI | 0.47 | 0.36 | 0.13 | -0.34 |
| HOU | -1.25 | -0.11 | 0.35 | 1.60 |
| IND | -2.13 | -1.42 | -0.72 | 1.41 |
| MIL | -2.18 | -1.49 | -0.65 | 1.53 |
| PHO | -1.76 | -2.33 | -2.44 | -0.68 |
| GSW | -3.92 | -2.77 | -2.95 | 0.97 |
| LAC | -3.17 | -2.96 | -2.67 | 0.50 |
| CHA | -2.31 | -3.72 | -4.63 | -2.31 |
| MIN | -2.62 | -4.71 | -5.16 | -2.53 |
| TOR | -5.86 | -4.78 | -4.17 | 1.69 |
| DET | -6.61 | -5.83 | -5.21 | 1.40 |
| NJN | -6.22 | -6.38 | -6.77 | -0.55 |
| WAS | -7.64 | -7.09 | -6.87 | 0.78 |
| SAC | -8.99 | -8.79 | -8.46 | 0.53 |
| CLE | -10.66 | -10.81 | -10.89 | -0.23 |
What can we interpret these to mean? If a team has a higher ^1 and a lower ^2, the have had a bunch of better performances and a few really bad clunkers. On the other hand, if the ^1 is lower and the ^2 is higher, they’ve had a bunch of lesser performances and a few really dominant ones. Basically, the difference reflects the skew of the distribution. Utah has generally been quite solid (median +5.68) but has had some awful clunkers (mean +2.35). On the other hand, Denver has typically played mediocre but every once in a while plays a great game.
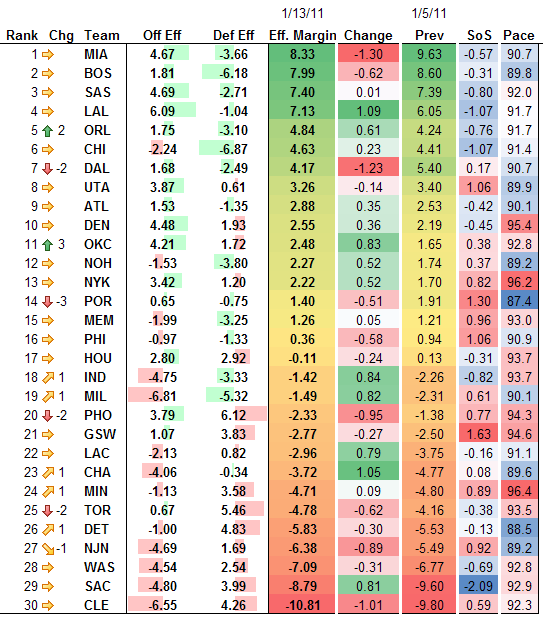
Okay, on to the actual rankings. The last time I did these was 8 days ago, so the “previous” data is from that point. As usual, these are adjusted for rest days, location, and opponent, all according to the residuals^2. First the pretty image:
Miami and Dallas have hit rough patches, and Phoenix and Cleveland have continued to tumble. Cleveland is REALLY bad, now. The top 4 teams have continued to separate from the rest of the field, but a new contender is making an impressive run, as Orlando’s climb continues. Remember, these rankings weight the whole season equally–Orlando has been a different team with the new lineup.
And now something new– a new Google Motion Chart! This one tracks the day-by-day efficiency ranking of each team, since the ratings had fairly stabilized around December 20th. At that point, also, the trade occurred between Phoenix and Orlando. Check out their different trajectories since then!
Finally, here is the data from this week in table form:
| Rank | Chg | Team | Off Eff | Def Eff | Eff. Margin | Change | Prev | SoS | Pace |
|---|---|---|---|---|---|---|---|---|---|
| 1 | MIA | 4.67 | -3.66 | 8.33 | -1.30 | 9.63 | -0.57 | 90.7 | |
| 2 | BOS | 1.81 | -6.18 | 7.99 | -0.62 | 8.60 | -0.31 | 89.8 | |
| 3 | SAS | 4.69 | -2.71 | 7.40 | 0.01 | 7.39 | -0.80 | 92.0 | |
| 4 | LAL | 6.09 | -1.04 | 7.13 | 1.09 | 6.05 | -1.07 | 91.7 | |
| 5 | 2 | ORL | 1.75 | -3.10 | 4.84 | 0.61 | 4.24 | -0.76 | 91.7 |
| 6 | CHI | -2.24 | -6.87 | 4.63 | 0.23 | 4.41 | -1.07 | 91.4 | |
| 7 | -2 | DAL | 1.68 | -2.49 | 4.17 | -1.23 | 5.40 | 0.17 | 90.7 |
| 8 | UTA | 3.87 | 0.61 | 3.26 | -0.14 | 3.40 | 1.06 | 89.9 | |
| 9 | ATL | 1.53 | -1.35 | 2.88 | 0.35 | 2.53 | -0.42 | 90.1 | |
| 10 | DEN | 4.48 | 1.93 | 2.55 | 0.36 | 2.19 | -0.45 | 95.4 | |
| 11 | 3 | OKC | 4.21 | 1.72 | 2.48 | 0.83 | 1.65 | 0.38 | 92.8 |
| 12 | NOH | -1.53 | -3.80 | 2.27 | 0.52 | 1.74 | 0.37 | 89.2 | |
| 13 | NYK | 3.42 | 1.20 | 2.22 | 0.52 | 1.70 | 0.82 | 96.2 | |
| 14 | -3 | POR | 0.65 | -0.75 | 1.40 | -0.51 | 1.91 | 1.30 | 87.4 |
| 15 | MEM | -1.99 | -3.25 | 1.26 | 0.05 | 1.21 | 0.96 | 93.0 | |
| 16 | PHI | -0.97 | -1.33 | 0.36 | -0.58 | 0.94 | 1.06 | 90.9 | |
| 17 | HOU | 2.80 | 2.92 | -0.11 | -0.24 | 0.13 | -0.31 | 93.7 | |
| 18 | 1 | IND | -4.75 | -3.33 | -1.42 | 0.84 | -2.26 | -0.82 | 93.7 |
| 19 | 1 | MIL | -6.81 | -5.32 | -1.49 | 0.82 | -2.31 | 0.61 | 90.1 |
| 20 | -2 | PHO | 3.79 | 6.12 | -2.33 | -0.95 | -1.38 | 0.77 | 94.3 |
| 21 | GSW | 1.07 | 3.83 | -2.77 | -0.27 | -2.50 | 1.63 | 94.6 | |
| 22 | LAC | -2.13 | 0.82 | -2.96 | 0.79 | -3.75 | -0.16 | 91.1 | |
| 23 | 1 | CHA | -4.06 | -0.34 | -3.72 | 1.05 | -4.77 | 0.08 | 89.6 |
| 24 | 1 | MIN | -1.13 | 3.58 | -4.71 | 0.09 | -4.80 | 0.89 | 96.4 |
| 25 | -2 | TOR | 0.67 | 5.46 | -4.78 | -0.62 | -4.16 | -0.38 | 93.5 |
| 26 | 1 | DET | -1.00 | 4.83 | -5.83 | -0.30 | -5.53 | -0.13 | 88.5 |
| 27 | -1 | NJN | -4.69 | 1.69 | -6.38 | -0.89 | -5.49 | 0.92 | 89.2 |
| 28 | WAS | -4.54 | 2.54 | -7.09 | -0.31 | -6.77 | -0.69 | 92.8 | |
| 29 | SAC | -4.80 | 3.99 | -8.79 | 0.81 | -9.60 | -2.09 | 92.9 | |
| 30 | CLE | -6.55 | 4.26 | -10.81 | -1.01 | -9.80 | 0.59 | 92.3 |
Great Stuff. Looks like they gave the finalists tough rest day schedules!
Yes, they certainly did so far. I think it will even out more, though, as the season progresses.
Nice rankings. I’m not a huge stats guy, but those rankings look real accurate just by the eyeball test when I watch games. Nice site.
Nice work, Daniel. Is there a way to separate these efficiency rankings into home and away?