There are many ways to rank NBA teams; some better than others. This method runs as follows:
- Compile all game advanced team boxscores from Basketball Reference, like this one:
Four Factors Pace eFG% TOV% ORB% FT/FGA ORtg SAS 90.8 .506 13.8 32.6 .186 113.4 BOS 90.8 .647 15.5 18.5 .107 115.6 - Adjust efficiency differential in the game for location and rest days.
- Solve for each team’s efficiency differential by minimizing the residuals^1.5 for each game (using Excel Solver)
- Generate an offense-defense skew for each team by solving for average efficiency in games that team plays, adjusted for rest days (minimizing residuals^1.5 again).
- Use the offense-defense skew and the team’s efficiency differential to generate offensive and defensive ratings for each team.
- Apply the same methods to generate pace values for each team
So this method differs in a few ways from some others:
- It weights each GAME equally, rather than each possession (I don’t want a fast-paced OT game to mean more in the ratings than a slow game).
- I minimize residuals^1.5 rather than squared residuals. I suppose a true average would use squared residuals, but I liked the fact that using ^1.5 causes outliers to have less of an effect. Research is needed to figure out what is the proper approach–for retrospective ratings, ^2 is probably best, but for predictive perhaps something less than ^2. This was simply a judgment call on my part.
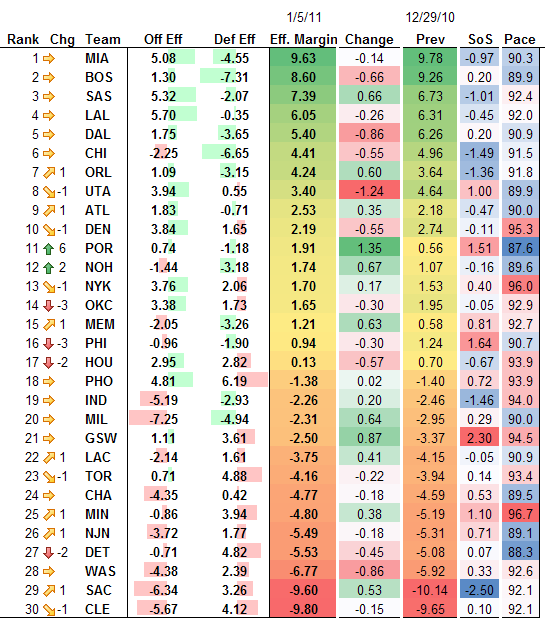
So anyway, here are the ratings. I’ll show them both in lovely Excel-conditional-formatting splendor (which would be a headache to code as CSS–only Ken Pomeroy has done it that I know of!) and then I’ll post them in table format as well for easy sorting and copying.
And for sorting and copying, here is the nice table form:
| Rank | Chg | Team | Off Eff | Def Eff | Eff. Margin | Change | Prev | SoS | Pace |
|---|---|---|---|---|---|---|---|---|---|
| 1 | MIA | 5.08 | -4.55 | 9.63 | -0.14 | 9.78 | -0.97 | 90.3 | |
| 2 | BOS | 1.30 | -7.31 | 8.60 | -0.66 | 9.26 | 0.20 | 89.9 | |
| 3 | SAS | 5.32 | -2.07 | 7.39 | 0.66 | 6.73 | -1.01 | 92.4 | |
| 4 | LAL | 5.70 | -0.35 | 6.05 | -0.26 | 6.31 | -0.45 | 92.0 | |
| 5 | DAL | 1.75 | -3.65 | 5.40 | -0.86 | 6.26 | 0.20 | 90.9 | |
| 6 | CHI | -2.25 | -6.65 | 4.41 | -0.55 | 4.96 | -1.49 | 91.5 | |
| 7 | 1 | ORL | 1.09 | -3.15 | 4.24 | 0.60 | 3.64 | -1.36 | 91.8 |
| 8 | -1 | UTA | 3.94 | 0.55 | 3.40 | -1.24 | 4.64 | 1.00 | 89.9 |
| 9 | 1 | ATL | 1.83 | -0.71 | 2.53 | 0.35 | 2.18 | -0.47 | 90.0 |
| 10 | -1 | DEN | 3.84 | 1.65 | 2.19 | -0.55 | 2.74 | -0.11 | 95.3 |
| 11 | 6 | POR | 0.74 | -1.18 | 1.91 | 1.35 | 0.56 | 1.51 | 87.6 |
| 12 | 2 | NOH | -1.44 | -3.18 | 1.74 | 0.67 | 1.07 | -0.16 | 89.6 |
| 13 | -1 | NYK | 3.76 | 2.06 | 1.70 | 0.17 | 1.53 | 0.40 | 96.0 |
| 14 | -3 | OKC | 3.38 | 1.73 | 1.65 | -0.30 | 1.95 | -0.05 | 92.9 |
| 15 | 1 | MEM | -2.05 | -3.26 | 1.21 | 0.63 | 0.58 | 0.81 | 92.7 |
| 16 | -3 | PHI | -0.96 | -1.90 | 0.94 | -0.30 | 1.24 | 1.64 | 90.7 |
| 17 | -2 | HOU | 2.95 | 2.82 | 0.13 | -0.57 | 0.70 | -0.67 | 93.9 |
| 18 | PHO | 4.81 | 6.19 | -1.38 | 0.02 | -1.40 | 0.72 | 93.9 | |
| 19 | IND | -5.19 | -2.93 | -2.26 | 0.20 | -2.46 | -1.46 | 94.0 | |
| 20 | MIL | -7.25 | -4.94 | -2.31 | 0.64 | -2.95 | 0.29 | 90.0 | |
| 21 | GSW | 1.11 | 3.61 | -2.50 | 0.87 | -3.37 | 2.30 | 94.5 | |
| 22 | 1 | LAC | -2.14 | 1.61 | -3.75 | 0.41 | -4.15 | -0.05 | 90.9 |
| 23 | -1 | TOR | 0.71 | 4.88 | -4.16 | -0.22 | -3.94 | 0.14 | 93.4 |
| 24 | CHA | -4.35 | 0.42 | -4.77 | -0.18 | -4.59 | 0.53 | 89.5 | |
| 25 | 1 | MIN | -0.86 | 3.94 | -4.80 | 0.38 | -5.19 | 1.10 | 96.7 |
| 26 | 1 | NJN | -3.72 | 1.77 | -5.49 | -0.18 | -5.31 | 0.71 | 89.1 |
| 27 | -2 | DET | -0.71 | 4.82 | -5.53 | -0.45 | -5.08 | 0.07 | 88.3 |
| 28 | WAS | -4.38 | 2.39 | -6.77 | -0.86 | -5.92 | 0.33 | 92.6 | |
| 29 | 1 | SAC | -6.34 | 3.26 | -9.60 | 0.53 | -10.14 | -2.50 | 92.1 |
| 30 | -1 | CLE | -5.67 | 4.12 | -9.80 | -0.15 | -9.65 | 0.10 | 92.1 |
These are great. How much effect do the rest days have on your ratings?
It would be neat to see a study that looked at the best exponent for prediction. Any preliminary study/intuition for why you think 1.5 would be better?
Rest days research can be found at: http://sonicscentral.com/apbrmetrics/viewtopic.php?p=32743#32743
Sometime soon perhaps I’ll do an article on the rest days analysis and its impact.
The 1.5 is just a gut feeling–2 is proper for a true mean value, but I kind of like the effect of diminishing outliers found by using 1.5 as the exponent. Neil Paine looked at ^1 vs. ^2 and found ^2 is more predictive.
Thanks Daniel. I’m familiar with and enjoyed the thread, but I was wondering how much effect rest days had on the current ratings. That is, if you run the same model without rest days, is Miami a 9.65 rather than a 9.63 or do the schedules differ enough so that the effect is larger than that?
I’ve liked your work on apbrmetrics and am glad to see the blog.
I guess if compare your ratings with Neal’s on the same day, I’d have my answer?
No, Neil is minimizing residuals^2. I’ll run the numbers for you and post, okay? I’ll update these rankings on the 13th at the latest.
Oh yeah, I temporarily forgot about the 1.5 vs. 2. Thanks! The results should be interesting.