A couple of months ago, I introduced my method of With-or-Without-You(WOWY) for the NBA. This time, I’ll revise and expand upon the method, and take a pre-playoff look at the hottest team going: the Chicago Bulls.
As Kevin Pelton chronicled, the Bulls have actually been quite healthy this year–only Joakim Noah and Carlos Boozer have missed significant time, among the regulars in the rotation. Kurt Thomas has missed time, also, but he has also been sat by Tom Thibodeau when healthy–complicating any analysis of WOWY. For this analysis, I’ll focus on Noah and Boozer.
The basic concept of WOWY is to compare the team’s production with and without a given player. In order to get a decent read from the analysis, several things are required:
- A decent sample-size both with and without the player
- Opponent/rest/location adjusted game efficiencies
- No collinearity of multiple players (can’t have multiple players with identical or mirror-image in/out patterns; this often happens with multi-player trades.)
The Bulls with Noah and Boozer are a perfect candidate. I’m going to do the analysis 3 ways.
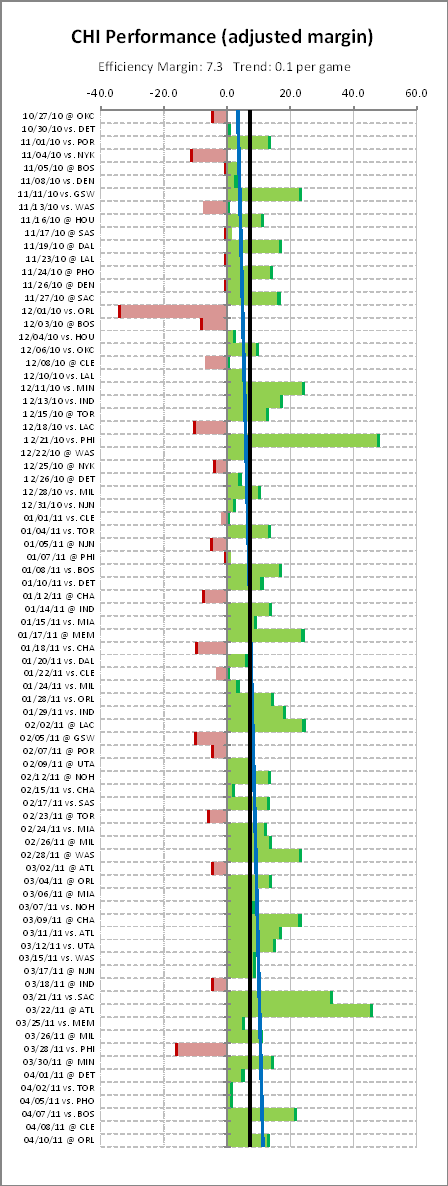
First, here are 2 charts of the Bulls’ performances this year (hang on–they’re long):
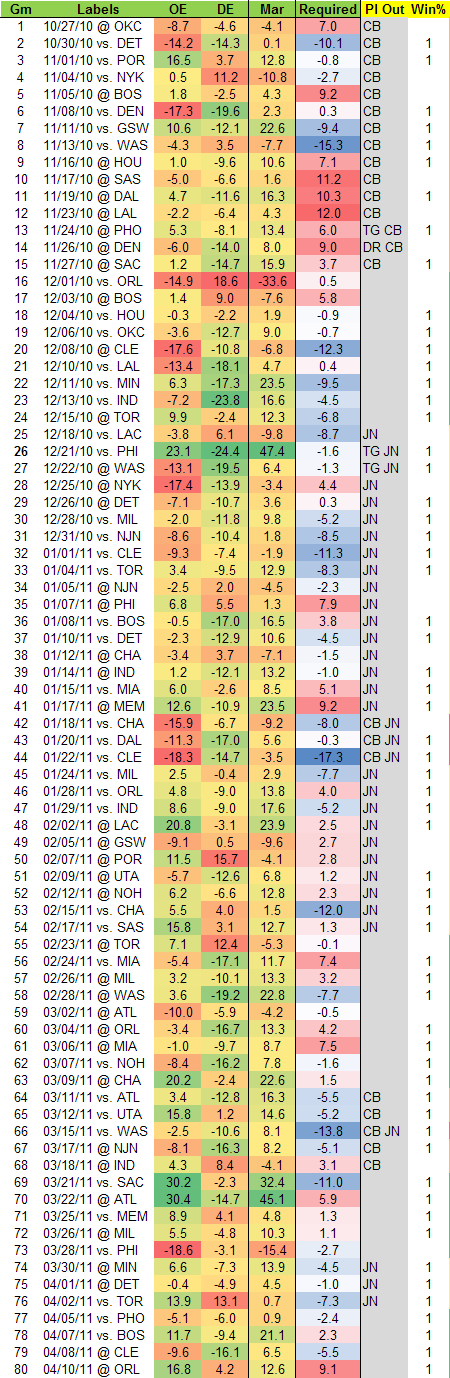
Okay, that was a bunch of data. The first chart is mostly just cool to look at; the second chart is where the meat is. We have the offensive, defensive, and overall efficiencies, the difficulty of the game (“required”), who was missing, and whether the Bulls won or not.
Notice, I also showed when Derrick Rose and Taj Gibson were out. Neither of them were out enough games to get meaningful results from this analysis.
I ran 3 different regressions to estimate how good the Bulls are with and without Boozer and Noah. The first is basic: no weighting, nothing. Just simple math:
| Eff Mar | Off Eff | Def Eff | |
|---|---|---|---|
| Team | 9.0 | 2.6 | -6.4 |
| Carlos Boozer | 3.2 | 4.4 | 1.2 |
| Joakim Noah | 2.0 | 1.6 | -0.3 |
Okay, that was easy. The Bulls are better when they have Boozer and Noah! I could have guessed that.
These numbers are basically VORP, of what VORP is supposed to be: the player’s value to the team (though VORP assumes a league-average team). Noah may be underrated by this, league-wide, because he has very good replacements on the Bulls team.
Now, it isn’t the case here, but often times the numbers can be very large from a regression like this, because it’s such a small sample size. To combat that, I add a weighting factor toward league-average for each player. I basically add in several games where the players have league-average impacts. That’s still above 0 because of the replacement-level consideration. I ran through a bunch of regressions, doing out-of-sample tests for a number of teams, to hone in on the best weighting factor. I ended up with using 30 games of league average for best out-of-sample prediction quality. Yes, that is a very strong regression to the mean–but it shows how wonky WOWY numbers really can be. In other words, be wary of using raw WOWY numbers.
Okay, here’s the same pair of Boozer and Noah using the modified, regressed-to-the-mean WOWY:
| Eff Mar | Off Eff | Def Eff | |
|---|---|---|---|
| Team | 8.9 | 2.0 | -6.9 |
| Carlos Boozer | 2.7 | 2.6 | 0.0 |
| Joakim Noah | 2.2 | 1.5 | -0.7 |
Wow. That looks really similar! Well, the total effects are similar. Boozer no longer looks quite so lop-sided offensively vs. defensively. He’s still a replacement-level defender by this measure as opposed to a REALLY bad defender before.
But now–here I am weighting every game the same. How about some Bayesian stuff here!
Well, a while back I determined the appropriate Bayesian weights to de-emphasize older game results for the best future predictive accuracy. How about I just port those weights into the WOWY regression directly? That’s what I did. I left the 30 games of regression-to-the-mean for each player in… but what I’m interested in now is the predictive accuracy of the TEAM number. The 8.9 in the last regression. Here are the Bayesian WOWY results:
| Eff Mar | Off Eff | Def Eff | |
|---|---|---|---|
| Team | 10.0 | 3.5 | -6.5 |
| Carlos Boozer | 2.7 | 2.8 | 0.0 |
| Joakim Noah | 2.7 | 1.7 | -1.1 |
10.0. Uh… wow. That’s scary! No wonder the Bulls look like favorites now in the East! In other words, my best estimate of their future efficiency differential is +10.0, a mark reached for a season by only a handful of teams in history (several of them Bulls teams). And in the playoffs, the rotations will be tightened further (bad players play less), so the actual efficiency diffential would be higher. (That effect may be weaker for the Bulls than for shallow teams, so their relative efficiency to other playoff teams may actually drop some.)
What have we seen? WOWY provides a good glimpse of how much Boozer and Noah mean to the Bulls, and it also provides an excellent improvement to the Bayesian power ratings by adjusting for injuries on the team.
Watch out for the Bulls!
Coming soon: some other interesting playoff team WOWY calc’s (the Bulls were just the easiest!).
Stathead » Blog Archive
[…] Daniel M looks at Boozer and Noah’s impacts on the Bulls. Link Posted on Tuesday, April 12th, 2011 at 5:44 pm, Category: Basketball, Tags: carlos-boozer, […]
Awesome! I haven’t seen your WOWY before and found it really cool. I look forward to the upcoming stuff. How large are the standard errors?
Must be big if you need 30 games of avg. for best out-of-sample results! I haven’t put any of these regressions in R yet, so I don’t know the numbers.
This may be MOST valuable as a way of adjusting the team-level Bayesian, honestly. It can also validate replacement level for +/- if used on a large enough scale.
Wowy! Lots of cool stuff here, as always. Interesting that you think tightened rotations will drive the Bulls up, when they don’t have a top 5-man rotation…
Curious to see how other teams look by this method.
Tightened rotations will help every team (presuming the players they play the most are their best players!), but you’re right–it won’t help the Bulls as much as other teams (like the Celtics, Lakers, Heat, and Spurs).