The study of football is much more tricky than that of basketball–there are more players on the field and fewer plays and games to study. The links in the sidebar list a few of the sites that have done good work studying football statistics.
Since the players are hard to analyze, I have confined myself primarily to studying team-level play. I have developed two frameworks for analyzing and ranking teams.
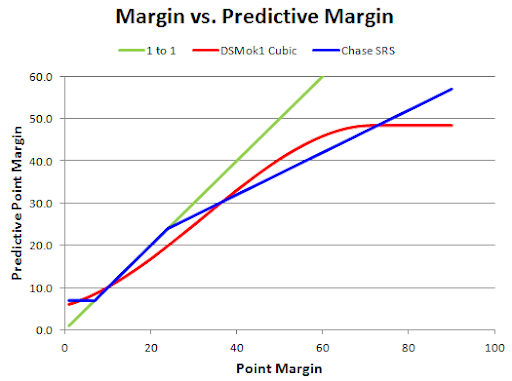
The first is a basic points-based approach. Who beat whom, and by how much? Of course, I didn’t just stick to the points. I analyzed game margins to determine how much to regress the games to be maximally predictive of the rest of the season. The approach I took was to reduce the points for large margins, but increase it for small margins. So a 1 point win is actually worth 6 points or so in my system, a 10 point win worth 10 points, a 20 point win worth about 16 and so on. Chase Stuart has used a similar approach in his Simple Rating System of NCAA Football for Pro Football Reference. To generate my numbers, I fitted a cubic curve to predict the last 3 or 4 games of the year from the first 8 or 9, over the past several years. My “effective points” vs. actual margin are shown in the chart below:
To generate rankings of all of the teams in the NCAA, I simply took all of the games this year (thanks to College Football Reference for the data) and recursively generated ratings by adjusting for opponent, then updating, and adjusting for opponent again using the new ratings until the results converged. This is the approach discussed as the “Simple Rating System”.
So now, to the results. These are the current ratings updated through the Sugar Bowl:
| Rank | Team | Points | SOS |
|---|---|---|---|
| 1 | Oregon | 28.8 | 4.3 |
| 2 | Stanford | 26.3 | 6.6 |
| 3 | Boise State | 25.6 | -0.6 |
| 4 | Texas Christian | 23.8 | -1.0 |
| 5 | Alabama | 21.7 | 4.5 |
| 6 | Auburn | 21.0 | 5.1 |
| 7 | Ohio State | 19.9 | 0.0 |
| 8 | Oklahoma | 19.2 | 5.6 |
| 9 | Oklahoma State | 17.4 | 2.6 |
| 10 | Wisconsin | 16.9 | 0.5 |
| 11 | Arkansas | 16.3 | 5.4 |
| 12 | Florida State | 14.6 | 5.3 |
| 13 | Louisiana State | 14.1 | 4.6 |
| 14 | Missouri | 13.8 | 2.6 |
| 15 | Nevada | 13.7 | -3.7 |
| 16 | Virginia Tech | 13.5 | 3.1 |
| 17 | Texas A&M | 13.1 | 3.9 |
| 18 | South Carolina | 12.6 | 6.9 |
| 19 | Southern California | 12.6 | 8.6 |
| 20 | Utah | 12.5 | 0.9 |
| 21 | Nebraska | 12.3 | 1.8 |
| 22 | Arizona | 12.0 | 8.2 |
| 23 | Arizona State | 11.9 | 7.0 |
| 24 | North Carolina State | 11.5 | 2.7 |
| 25 | Mississippi State | 11.0 | 3.4 |
Oregon blew people out, and so did Stanford. This points-based approach loves Oregon’s scoring, and penalizes Auburn for scraping out close wins.
However…
I also have another rating system. This other system looks at yards-per-play, interceptions, and fumbles, regressed appropriately. For this method, I got data from NCAA.org, which has all of the information you’ll ever need for each team. An example table of those I pulled is for Air Force’s Offense.
So, how would one rank teams based on yards-per-play? Well, the basic rating would be simply to solve recursively for each team’s opponent-adjusted offensive and defensive yards-per-play. Then add in the value of each interception and fumble.
I was a little more tricky. I ran fudged split-half correlations for yards-per-play, int/play, and fumble/play. I say fudged because I split it into halves of the season, rather than into, say, even plays and odd plays. I then took that correlation value and generated a regression rate base on it, following TangoTiger’s approach for baseball. See this headache-inducing post of his.
The regression rates I got:
| Off YPP | O Int/Play | O Fum/Play | Def YPP | D Int/Play | D Fum/Play |
|---|---|---|---|---|---|
| 205 | 1553 | 4638 | 182 | 1548 | 30469 |
Okay, so what does that mean? Well, if you have the numbers of NCAA-average plays to add to regress properly. If I’ve seen 700 plays of Auburn’s, after I generate Auburn’s opposition-adjusted yards-per-play, I then add 205 plays of average offensive yards-per-play to their numbers to predict Auburn’s future yards-per-play. It’s just a mathematically-more-rigorous form of regression-to-the-mean.
Next, one has to translate the interceptions and fumbles into yards. Interceptions are worth about 45 yards, I found, and fumbles about 15 (I’m using total fumbles, not fumbles lost, so that would be about 30 yards per fumble lost). Finally, the adjusted final yards-per-play ratings must be translated to points. I’m using 7.75 points per yard-per-play advantage.
So, now I have run this yards-per-play rating system, and what do the numbers show?
| Rank | Team | YPP Mar | Points | Off YPP | O Int | O Fum | Def YPP | D Int | D Fum |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Alabama | 2.89 | 22.4 | 7.0 | 1.1% | 2.4% | 4.4 | 1.8% | 2.4% |
| 2 | Boise St. | 2.82 | 21.9 | 6.8 | 1.2% | 2.4% | 4.2 | 1.5% | 2.5% |
| 3 | Auburn | 2.65 | 20.6 | 7.4 | 1.2% | 2.3% | 4.9 | 1.4% | 2.4% |
| 4 | Arkansas | 2.47 | 19.1 | 7.3 | 1.5% | 2.4% | 4.9 | 1.6% | 2.4% |
| 5 | Oregon | 2.37 | 18.3 | 6.7 | 1.1% | 2.4% | 4.6 | 1.8% | 2.4% |
| 6 | Stanford | 1.88 | 14.6 | 6.6 | 1.2% | 2.2% | 5.1 | 1.9% | 2.5% |
| 7 | TCU | 1.86 | 14.4 | 6.3 | 1.3% | 2.3% | 4.6 | 1.5% | 2.4% |
| 8 | Ohio St. | 1.81 | 14.0 | 6.2 | 1.6% | 2.2% | 4.5 | 1.7% | 2.5% |
| 9 | South Carolina | 1.74 | 13.5 | 6.4 | 1.5% | 2.4% | 4.7 | 1.4% | 2.4% |
| 10 | Oklahoma St. | 1.72 | 13.3 | 6.5 | 1.4% | 2.4% | 4.9 | 1.6% | 2.4% |
| 11 | Georgia | 1.69 | 13.1 | 6.4 | 1.2% | 2.4% | 4.9 | 1.6% | 2.4% |
| 12 | Nebraska | 1.62 | 12.6 | 6.2 | 1.1% | 2.8% | 4.8 | 1.7% | 2.4% |
| 13 | Arizona | 1.55 | 12.0 | 6.2 | 1.2% | 2.3% | 4.8 | 1.5% | 2.4% |
| 14 | LSU | 1.54 | 11.9 | 5.8 | 1.3% | 2.5% | 4.5 | 1.8% | 2.4% |
| 15 | Iowa | 1.41 | 10.9 | 5.9 | 1.2% | 2.3% | 4.8 | 1.8% | 2.4% |
| 16 | Florida St. | 1.35 | 10.4 | 6.2 | 1.2% | 2.5% | 5.0 | 1.5% | 2.4% |
| 17 | Hawaii | 1.31 | 10.1 | 6.7 | 1.5% | 2.4% | 5.5 | 1.8% | 2.4% |
| 18 | Virginia Tech | 1.28 | 9.9 | 6.3 | 1.1% | 2.3% | 5.4 | 1.9% | 2.4% |
| 19 | Texas A&M | 1.19 | 9.2 | 5.7 | 1.3% | 2.5% | 4.6 | 1.6% | 2.4% |
| 20 | Florida | 1.18 | 9.1 | 5.5 | 1.3% | 2.7% | 4.5 | 2.0% | 2.4% |
| 21 | Miami (FL) | 1.13 | 8.7 | 6.2 | 1.9% | 2.4% | 4.9 | 1.6% | 2.4% |
| 22 | Mississippi St. | 1.11 | 8.6 | 5.7 | 1.4% | 2.4% | 4.7 | 1.6% | 2.4% |
| 23 | North Carolina | 1.10 | 8.5 | 5.9 | 1.3% | 2.4% | 5.0 | 1.7% | 2.4% |
| 24 | Oklahoma | 1.07 | 8.3 | 5.8 | 1.2% | 2.3% | 5.0 | 1.7% | 2.4% |
| 25 | Wisconsin | 1.06 | 8.2 | 6.3 | 1.2% | 2.3% | 5.4 | 1.6% | 2.4% |
Wow, that looks a little different than the points-based ranking! Now the SEC dominates the list, rather than the Pac 10.
Comparing Oregon and Auburn: Yards-Per-Play has Auburn favored by 2 1/2; SRS-Points has Oregon favored by 7 1/2. Which is right? I don’t know. Other points-based rankings typically have Oregon ahead, like I do here. Sagarin does; Team Rankings does; so do the Massey Ratings. Other play-by-play rankings (F/+) like Auburn better, as my Yards-Per-Play ratings do.
Either way, this promises to be an exciting and balanced BCS championship game. The two best undefeated teams are here. Of course, Boise St. is probably their match, and Alabama (how DID they lose 3 games?) is also right there. But those 2 lost, so they are out.
Oregon-Auburn, here we come!
Read the full NCAA Pre-Title Game Ratings here, showing both SRS-Points and Yards-Per-Play. P.S. They aren’t sortable, but they are full of pretty colors!