Last week I posted my NCAA Bayesian Ratings and methodology. Today I thought I’d update the numbers quickly and add a new twist.
What is the objective in basketball? To win the game! When doing a predictive rating system (like this Bayesian method) or even trying to tell how good teams are over this season (KenPom’s ratings), we account for margin of victory rather than just wins and losses. To be perfectly “just,” when choosing who should be in the NCAA tournament, why should we look at margin of victory? I’m going to craft a rating system here that doesn’t look at margin of victory at all. I’ll call it DSMRPI, since the RPI system is what it would supersede.
Ken Pomeroy lists each team’s opponent strength as a Pythagorean winning percentage (against average foes). We also can easily calculate each team’s winning percentage. How does one merge the two into an overall win%? Just convert the win percentages into a Z-score, sum, and convert back into a win%. Normsdist(Normsinv(Win%)+Normsinv(OppPyth%)). Easy!
The top 10 teams:
| Rank | Team | Win% | Opp% | RPI% |
|---|---|---|---|---|
| 1 | Ohio St. | 93.5% | 73.8% | 98.4% |
| 2 | Kansas | 93.5% | 69.9% | 97.9% |
| 3 | San Diego St. | 93.5% | 69.6% | 97.9% |
| 4 | Brigham Young | 90.3% | 67.4% | 96.0% |
| 5 | Duke | 87.1% | 72.9% | 95.9% |
| 6 | Pittsburgh | 87.1% | 72.3% | 95.8% |
| 7 | Purdue | 80.6% | 77.3% | 94.7% |
| 8 | Notre Dame | 83.3% | 73.9% | 94.6% |
| 9 | North Carolina | 80.0% | 77.5% | 94.5% |
| 10 | Syracuse | 80.6% | 73.8% | 93.4% |
Except… what happens if a team has never lost or has never won? Then Normsinv() is undefined, because the Z-score is either +infinity or -infinity. Great.
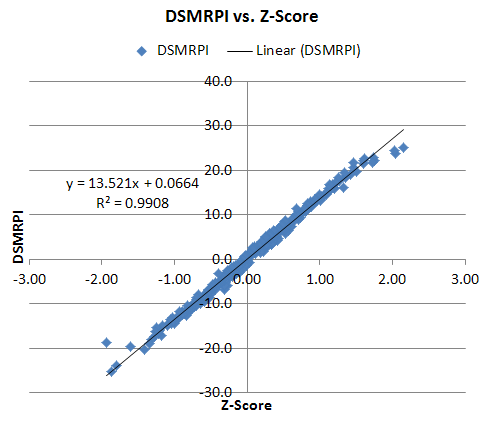
So here’s an alternate approach: assign each win a constant value and each loss a constant value (the same value). Sum those values, and add to the opponent efficiency differential to create an overall “efficiency differential” only based on opponent strength and win-loss record. To hone those constant values for the wins and losses, I maximized the correlation between the new number and the Z-scores calculated previously, as well as the correlation of the rank orders of the new number and the z-score.
A number between 18 and 21 for the value of a win works the best; I’ll use 20 just for simplicity’s sake. There isn’t much of a difference within that region. So I’m multiplying all wins by 20 and all losses by -20, thus assuming a margin of victory of 20 in all games. This harms teams with outlying records, but I think the Z-score is actually less valid than this method with teams with records like 29-1.
So the final DSMRPI ratings look like this:
| Team | Conf | W-L | SoS Pyth | DSMRPI |
|---|---|---|---|---|
| Ohio St. | B10 | 29-2 | 73.8% | 25.2 |
| San Diego St. | MWC | 29-2 | 69.6% | 24.5 |
| Kansas | B12 | 29-2 | 69.9% | 23.7 |
| Duke | ACC | 27-4 | 72.9% | 22.9 |
| Purdue | B10 | 25-6 | 77.3% | 22.6 |
| North Carolina | ACC | 24-6 | 77.5% | 22.3 |
| Brigham Young | MWC | 28-3 | 67.4% | 22.2 |
| Georgetown | BE | 21-9 | 82.5% | 21.8 |
| Pittsburgh | BE | 27-4 | 72.3% | 21.7 |
| Notre Dame | BE | 25-5 | 73.9% | 21.4 |
Kansas is below San Diego St. because they played more home games, tweaking their SoS and overall value downward.
So now, with DSMRPI in hand we have a good idea of who SHOULD get into the NCAA tournament. I have added an automatic seeding capability to my spreadsheet, along with a few other cool tweaks.
I also added a “Heat” column, showing how the Bayesian Rating has changed over the last 10 games.
Open the FULL SPREADSHEET for all of the bells and whistles!
| Rank | Team | Conf | Win-Loss | KenPom | Bayesian | Heat | DSMRPI | Rank | Seed |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Ohio St. | B10 | 29-2 | 37.2 | 34.55 | 1.22 | 25.2 | 1 | 1 |
| 2 | Kansas | B12 | 29-2 | 32.8 | 30.88 | 1.46 | 23.7 | 3 | 1 |
| 3 | Duke | ACC | 27-4 | 31.7 | 29.69 | 0.30 | 22.9 | 4 | 1 |
| 4 | Pittsburgh | BE | 27-4 | 29.5 | 28.03 | 0.47 | 21.7 | 9 | 3 |
| 5 | Purdue | B10 | 25-6 | 29 | 27.51 | 3.45 | 22.6 | 5 | 2 |
| 6 | Wisconsin | B10 | 23-7 | 29.4 | 26.81 | -0.03 | 20.7 | 11 | 3 |
| 7 | Texas | B12 | 25-6 | 28.4 | 26.66 | -1.56 | 19.1 | 14 | 4 |
| 8 | Syracuse | BE | 25-6 | 25.9 | 24.68 | 3.31 | 19.7 | 12 | 3 |
| 9 | Kentucky | SEC | 22-8 | 26.5 | 24.58 | -1.85 | 17.1 | 20 | 5 |
| 10 | Brigham Young | MWC | 28-3 | 27.2 | 24.54 | -0.38 | 22.2 | 7 | 2 |
| 11 | North Carolina | ACC | 24-6 | 25.2 | 23.92 | 3.65 | 22.3 | 6 | 2 |
| 12 | San Diego St. | MWC | 29-2 | 25.8 | 23.72 | 1.91 | 24.5 | 2 | 1 |
| 13 | Notre Dame | BE | 25-5 | 25 | 23.17 | 4.33 | 21.4 | 10 | 3 |
| 14 | Washington | P10 | 20-10 | 24 | 22.73 | -4.86 | 13.8 | 36 | 9 |
| 15 | Louisville | BE | 23-8 | 23 | 22.07 | 1.74 | 15.9 | 27 | 7 |
| 16 | Cincinnati | BE | 24-7 | 22.1 | 21.33 | 1.40 | 15.6 | 29 | 8 |
| 17 | Utah St. | WAC | 28-3 | 23.1 | 21.31 | 2.84 | 16.2 | 25 | 7 |
| 18 | Florida | SEC | 24-6 | 22.9 | 20.92 | 2.30 | 18.5 | 16 | 4 |
| 19 | Illinois | B10 | 19-12 | 22.3 | 20.86 | 0.62 | 16.5 | 23 | 6 |
| 20 | Belmont | ASun | 30-4 | 22.1 | 20.74 | 1.99 | 11.0 | 58 | 14 |
| 21 | West Virginia | BE | 20-10 | 21.9 | 20.58 | -0.79 | 19.5 | 13 | 4 |
| 22 | Vanderbilt | SEC | 21-9 | 20.6 | 19.23 | 0.43 | 14.8 | 31 | 8 |
| 23 | Georgetown | BE | 21-9 | 20.3 | 19.09 | -3.50 | 21.8 | 8 | 2 |
| 24 | Nevada Las Vegas | MWC | 23-7 | 20.1 | 19.07 | -0.03 | 17.3 | 19 | 5 |
| 25 | Arizona | P10 | 25-6 | 20.1 | 18.99 | -2.27 | 18.8 | 15 | 4 |
| 26 | Connecticut | BE | 21-9 | 20.1 | 18.85 | -1.96 | 17.8 | 18 | 5 |
| 27 | Villanova | BE | 21-10 | 20.7 | 18.74 | -3.50 | 16.8 | 21 | 6 |
| 28 | Missouri | B12 | 22-9 | 20.4 | 18.35 | -0.62 | 13.2 | 42 | 11 |
| 29 | St. John's | BE | 20-10 | 19.2 | 18.27 | 4.43 | 18.3 | 17 | 5 |
| 30 | George Mason | CAA | 26-6 | 19.7 | 18.27 | 0.33 | 13.5 | 37 | 10 |
| 31 | Kansas St. | B12 | 22-9 | 19.9 | 18.20 | 5.44 | 16.1 | 26 | 7 |
| 32 | Xavier | A10 | 24-6 | 18.6 | 17.68 | 1.53 | 16.4 | 24 | 6 |
| 33 | Marquette | BE | 18-13 | 19.4 | 17.56 | -1.51 | 10.8 | 59 | -- |
| 34 | Gonzaga | WCC | 23-9 | 18.1 | 17.17 | 2.62 | 10.3 | 62 | -- |
| 35 | Virginia Tech | ACC | 19-10 | 17.9 | 17.03 | -1.23 | 12.9 | 43 | 11 |
| 36 | Maryland | ACC | 18-13 | 18.2 | 16.98 | -3.92 | 7.3 | 83 | -- |
| 37 | Clemson | ACC | 20-10 | 17.9 | 16.80 | 1.13 | 11.8 | 53 | -- |
| 38 | Temple | A10 | 24-6 | 17.5 | 16.77 | 0.26 | 15.8 | 28 | 7 |
| 39 | UCLA | P10 | 22-9 | 16.7 | 16.13 | 5.31 | 15.0 | 30 | 8 |
| 40 | St. Mary's | WCC | 24-7 | 17 | 15.77 | -6.08 | 11.8 | 54 | 13 |
| 41 | Florida St. | ACC | 21-9 | 15.8 | 15.40 | -1.34 | 14.6 | 32 | 8 |
| 42 | New Mexico | MWC | 20-11 | 16.9 | 15.29 | 2.19 | 10.2 | 63 | -- |
| 43 | Michigan | B10 | 19-12 | 16.1 | 15.16 | 5.10 | 14.3 | 34 | 9 |
| 44 | Southern California | P10 | 18-13 | 16.1 | 15.03 | 1.02 | 12.0 | 51 | -- |
| 45 | Texas A&M | B12 | 23-7 | 15.5 | 14.58 | -1.64 | 14.5 | 33 | 9 |
| 46 | Richmond | A10 | 24-7 | 15.5 | 14.44 | -1.35 | 12.5 | 46 | 12 |
| 47 | Old Dominion | CAA | 26-6 | 15 | 14.35 | 3.13 | 13.4 | 39 | 10 |
| 48 | Michigan St. | B10 | 17-13 | 15.8 | 14.35 | -1.04 | 16.7 | 22 | 6 |
| 49 | Nebraska | B12 | 19-11 | 15.4 | 14.22 | -1.19 | 7.3 | 84 | -- |
| 50 | Washington St. | P10 | 19-11 | 15 | 14.21 | -2.81 | 11.5 | 55 | -- |
| 51 | UAB | CUSA | 22-7 | 15.1 | 14.05 | 2.27 | 13.4 | 38 | 10 |
| 52 | Iona | MAAC | 22-10 | 15.2 | 14.01 | 4.86 | 6.4 | 98 | 15 |
| 53 | Penn St. | B10 | 16-13 | 15.7 | 13.99 | 1.86 | 14.0 | 35 | 9 |
| 54 | Tennessee | SEC | 18-13 | 14.4 | 13.99 | -0.90 | 12.1 | 49 | 13 |
| 55 | Seton Hall | BE | 13-17 | 13.8 | 13.89 | 5.38 | 8.7 | 74 | -- |
| 56 | Butler | Horz | 22-9 | 14.4 | 13.58 | 0.53 | 12.0 | 50 | 13 |
| 57 | Boston College | ACC | 19-11 | 14.9 | 13.53 | 2.24 | 13.2 | 41 | 11 |
| 58 | Minnesota | B10 | 17-13 | 14.2 | 13.42 | -2.68 | 13.3 | 40 | 10 |
| 59 | Georgia | SEC | 20-10 | 14.3 | 13.38 | -0.79 | 12.8 | 44 | 11 |
| 60 | Alabama | SEC | 20-10 | 14.4 | 13.23 | -0.93 | 8.0 | 78 | -- |
| 61 | Duquesne | A10 | 18-11 | 13.7 | 13.10 | -3.32 | 6.7 | 92 | -- |
| 62 | Colorado | B12 | 19-12 | 14.9 | 12.77 | 1.55 | 9.4 | 70 | -- |
| 63 | Miami FL | ACC | 18-13 | 13.7 | 12.52 | 0.24 | 9.9 | 67 | -- |
| 64 | Wichita St. | MVC | 24-8 | 13.5 | 12.44 | -1.81 | 7.7 | 80 | -- |
| 65 | California | P10 | 17-13 | 13.4 | 12.19 | 1.11 | 11.9 | 52 | -- |
| 66 | Northwestern | B10 | 17-12 | 13.2 | 11.70 | -1.94 | 11.4 | 57 | -- |
| 67 | Colorado St. | MWC | 19-11 | 10.9 | 11.11 | -0.39 | 12.5 | 45 | 12 |
| 68 | Texas El Paso | CUSA | 23-8 | 11.8 | 10.60 | -0.26 | 9.5 | 69 | -- |
| 69 | Oakland | Sum | 23-9 | 11.4 | 10.60 | -2.53 | 11.4 | 56 | 13 |
| 70 | Baylor | B12 | 18-12 | 12.2 | 10.09 | -3.28 | 6.5 | 97 | -- |
| 71 | College of Charleston | SC | 24-9 | 10.4 | 10.07 | 0.92 | 8.5 | 76 | 14 |
| 72 | Southern Mississippi | CUSA | 21-9 | 12 | 9.99 | 0.43 | 10.2 | 64 | -- |
| 73 | Cleveland St. | Horz | 26-8 | 11.1 | 9.97 | -3.80 | 12.3 | 48 | 12 |
| 74 | Mississippi | SEC | 19-12 | 10.9 | 9.94 | 0.28 | 6.7 | 91 | -- |
| 75 | Marshall | CUSA | 21-10 | 10 | 9.46 | 0.39 | 9.1 | 71 | -- |
| 76 | Harvard | Ivy | 23-5 | 10.6 | 9.34 | 1.39 | 12.3 | 47 | 12 |
| 77 | Missouri St. | MVC | 25-8 | 9.7 | 9.27 | -0.88 | 9.7 | 68 | -- |
| 78 | Indiana | B10 | 12-19 | 10.1 | 9.08 | -1.70 | 3.4 | 132 | -- |
| 79 | Iowa St. | B12 | 16-15 | 9.9 | 9.02 | -2.49 | 3.3 | 134 | -- |
| 80 | Rutgers | BE | 14-16 | 9.4 | 8.72 | 1.06 | 6.5 | 94 | -- |
| 81 | Boise St. | WAC | 19-11 | 9.1 | 8.56 | -0.31 | 6.2 | 101 | -- |
| 82 | Virginia Commonwealth | CAA | 23-10 | 9.2 | 8.49 | -1.56 | 10.3 | 61 | -- |
| 83 | Oklahoma St. | B12 | 18-12 | 8.7 | 8.44 | -0.06 | 10.2 | 66 | -- |
| 84 | Iowa | B10 | 11-19 | 8.7 | 8.28 | 1.44 | 4.0 | 127 | -- |
| 85 | Wofford | SC | 20-12 | 8.1 | 7.71 | 1.05 | 3.8 | 128 | -- |
| 86 | Tulsa | CUSA | 18-12 | 8.1 | 7.65 | 2.40 | 6.7 | 90 | -- |
| 87 | Central Florida | CUSA | 19-10 | 8 | 7.55 | -1.54 | 6.8 | 88 | -- |
| 88 | North Carolina St. | ACC | 15-15 | 8.1 | 7.45 | 0.20 | 6.5 | 96 | -- |
| 89 | Georgia Tech | ACC | 13-17 | 8.2 | 7.32 | -1.38 | 2.7 | 140 | -- |
| 90 | Providence | BE | 15-16 | 8.1 | 7.25 | -3.29 | 4.7 | 117 | -- |
| 91 | Virginia | ACC | 16-14 | 7.1 | 7.11 | 4.05 | 6.6 | 93 | -- |
| 92 | Princeton | Ivy | 23-6 | 7.2 | 6.83 | 0.66 | 10.7 | 60 | -- |
| 93 | Stanford | P10 | 15-15 | 7.2 | 6.78 | 0.47 | 4.9 | 114 | -- |
| 94 | Valparaiso | Horz | 23-11 | 5.9 | 6.58 | -2.94 | 9.0 | 72 | -- |
| 95 | Bucknell | Pat | 24-8 | 7.4 | 6.55 | -2.32 | 7.0 | 86 | 15 |
| 96 | Morehead St. | OVC | 24-9 | 7.3 | 6.34 | 2.82 | 6.2 | 99 | 15 |
| 97 | Coastal Carolina | BSth | 28-5 | 4.9 | 6.33 | -2.61 | 5.7 | 105 | -- |
| 98 | Drexel | CAA | 21-10 | 6.2 | 6.09 | -4.28 | 8.6 | 75 | -- |
| 99 | Long Beach St. | BW | 20-10 | 8.4 | 5.94 | 4.15 | 10.2 | 65 | 14 |
| 100 | Oregon | P10 | 14-16 | 6.8 | 5.87 | 2.75 | 4.1 | 124 | -- |
| 101 | Memphis | CUSA | 22-9 | 5.9 | 5.72 | -1.82 | 8.9 | 73 | -- |
| 102 | Fairfield | MAAC | 24-7 | 7 | 5.67 | -2.28 | 6.0 | 102 | -- |
| 103 | James Madison | CAA | 21-11 | 6.1 | 5.67 | -2.59 | 7.6 | 82 | -- |
| 104 | Portland | WCC | 20-11 | 6.1 | 5.58 | 0.70 | 7.6 | 81 | -- |
| 105 | Arkansas | SEC | 18-12 | 6.2 | 5.41 | -1.03 | 3.4 | 131 | -- |
| 106 | Indiana St. | MVC | 20-13 | 4.8 | 5.32 | 2.40 | 7.0 | 87 | 15 |
| 107 | South Dakota St. | Sum | 19-11 | 6.1 | 5.27 | -1.65 | 0.0 | 170 | -- |
| 108 | Dayton | A10 | 19-12 | 5.1 | 5.14 | -3.17 | 6.7 | 89 | -- |
| 109 | Buffalo | MAC | 17-12 | 5.3 | 4.95 | -3.42 | 0.5 | 166 | -- |
| 110 | Rider | MAAC | 23-10 | 5.5 | 4.94 | -0.80 | 6.2 | 100 | -- |
| 111 | East Tennessee St. | ASun | 22-11 | 4.7 | 4.77 | -0.61 | 5.8 | 104 | -- |
| 112 | Texas Tech | B12 | 13-18 | 5 | 4.54 | 4.97 | 1.7 | 153 | -- |
| 113 | Long Island | NEC | 26-5 | 4.6 | 4.50 | -0.27 | 7.1 | 85 | 14 |
| 114 | Creighton | MVC | 19-14 | 4.5 | 4.29 | 0.15 | 1.3 | 159 | -- |
| 115 | Arizona St. | P10 | 12-18 | 4.7 | 4.14 | 0.60 | 4.6 | 120 | -- |
| 116 | Montana | BSky | 20-9 | 4.4 | 4.12 | -2.92 | 5.3 | 107 | 16 |
| 117 | Northern Colorado | BSky | 19-10 | 4.2 | 4.06 | -1.35 | 4.1 | 126 | -- |
| 118 | St. Louis | A10 | 12-18 | 3.8 | 3.99 | 3.44 | -1.3 | 183 | -- |
| 119 | Northern Arizona | BSky | 19-11 | 3.7 | 3.97 | 0.71 | 1.4 | 158 | -- |
| 120 | New Mexico St. | WAC | 15-16 | 4.1 | 3.87 | 0.50 | 3.0 | 135 | -- |
| 121 | South Florida | BE | 9-22 | 3.7 | 3.87 | -0.97 | 2.1 | 148 | -- |
| 122 | Mississippi St. | SEC | 17-13 | 4.3 | 3.84 | 4.17 | 4.1 | 125 | -- |
| 123 | South Carolina | SEC | 14-15 | 3.8 | 3.83 | -1.60 | 5.0 | 112 | -- |
| 124 | Austin Peay | OVC | 20-13 | 2.7 | 3.79 | -2.75 | 2.3 | 144 | -- |
| 125 | Wright St. | Horz | 19-14 | 4.6 | 3.78 | -0.06 | 4.1 | 123 | -- |
| 126 | Oral Roberts | Sum | 18-14 | 3.7 | 3.78 | 3.30 | 2.6 | 142 | -- |
| 127 | Rhode Island | A10 | 18-12 | 4.2 | 3.72 | -0.23 | 6.5 | 95 | -- |
| 128 | Northern Iowa | MVC | 19-13 | 3.7 | 3.65 | -3.56 | 4.7 | 118 | -- |
| 129 | St. Peter's | MAAC | 19-13 | 3.7 | 3.42 | 3.49 | 5.2 | 109 | -- |
| 130 | Air Force | MWC | 15-14 | 5.1 | 3.34 | 0.44 | 5.0 | 113 | -- |
| 131 | Kent St. | MAC | 21-10 | 3.8 | 3.22 | -0.26 | 5.1 | 111 | -- |
| 132 | Idaho | WAC | 18-12 | 4 | 3.18 | 3.41 | 4.4 | 122 | -- |
| 133 | Akron | MAC | 19-12 | 3.1 | 3.08 | 3.14 | 1.8 | 151 | -- |
| 134 | Wisconsin Milwaukee | Horz | 19-12 | 2.9 | 3.08 | 3.32 | 7.8 | 79 | -- |
| 135 | Murray St. | OVC | 23-8 | 3.5 | 2.93 | 1.37 | 3.7 | 129 | -- |
| 136 | IUPUI | Sum | 19-13 | 3.1 | 2.77 | -0.58 | 5.9 | 103 | -- |
| 137 | St. Bonaventure | A10 | 16-13 | 2.7 | 2.68 | 2.54 | 4.5 | 121 | -- |
| 138 | Hofstra | CAA | 21-11 | 3 | 2.67 | 0.48 | 8.3 | 77 | -- |
| 139 | Detroit | Horz | 17-16 | 2.8 | 2.65 | 1.70 | 2.9 | 136 | -- |
| 140 | Utah | MWC | 13-17 | 2.7 | 2.58 | -1.95 | 5.7 | 106 | -- |
| 141 | NC Asheville | BSth | 19-13 | 2.5 | 2.22 | 0.35 | 0.5 | 165 | 17 |
| 142 | Davidson | SC | 17-14 | 0.2 | 2.14 | 0.02 | 0.9 | 160 | -- |
| 143 | Vermont | AE | 23-8 | 2.9 | 2.05 | -1.88 | 3.7 | 130 | 16 |
| 144 | Southern Methodist | CUSA | 17-13 | 2 | 2.04 | 3.59 | -1.1 | 181 | -- |
| 145 | Loyola Chicago | Horz | 16-15 | 1.9 | 1.93 | -0.83 | -1.4 | 186 | -- |
| 146 | Pacific | BW | 16-14 | 2.1 | 1.75 | -4.99 | 1.9 | 150 | -- |
| 147 | East Carolina | CUSA | 16-14 | 2.3 | 1.53 | -0.68 | 4.7 | 119 | -- |
| 148 | Robert Morris | NEC | 18-13 | 1.2 | 1.40 | 2.85 | 2.9 | 138 | -- |
| 149 | Weber St. | BSky | 18-11 | 0.6 | 1.39 | 3.29 | 2.7 | 139 | -- |
| 150 | George Washington | A10 | 17-13 | 1.6 | 1.10 | 3.67 | 2.5 | 143 | -- |
| 151 | Ohio | MAC | 17-14 | 1 | 1.07 | 2.17 | -1.4 | 187 | -- |
| 152 | Santa Clara | WCC | 19-14 | 1.5 | 1.03 | -1.39 | 2.0 | 149 | -- |
| 153 | Western Michigan | MAC | 19-11 | -0.1 | 0.90 | 3.98 | 1.6 | 154 | -- |
| 154 | Furman | SC | 22-10 | 1.1 | 0.88 | -4.25 | 4.8 | 116 | -- |
| 155 | Oklahoma | B12 | 13-17 | 2 | 0.77 | -0.16 | 2.9 | 137 | -- |
| 156 | Rice | CUSA | 13-17 | 1.7 | 0.73 | 1.83 | -0.7 | 177 | -- |
| 157 | Fresno St. | WAC | 14-16 | 1 | 0.70 | 2.74 | -0.2 | 172 | -- |
| 158 | Oregon St. | P10 | 10-19 | 0.3 | 0.60 | 1.61 | -1.4 | 185 | -- |
| 159 | Lipscomb | ASun | 17-13 | 0.3 | 0.55 | -1.68 | 2.6 | 141 | -- |
| 160 | San Francisco | WCC | 17-14 | 1.6 | 0.53 | 1.28 | 5.2 | 108 | -- |
| 161 | Wisconsin Green Bay | Horz | 14-18 | 0.3 | 0.42 | -0.59 | 1.8 | 152 | -- |
| 162 | Hawaii | WAC | 18-11 | 1.1 | 0.42 | 3.51 | 2.1 | 147 | -- |
| 163 | North Dakota St. | Sum | 14-15 | -1 | 0.34 | 1.26 | -3.8 | 221 | -- |
| 164 | Nevada | WAC | 12-18 | 0.9 | 0.30 | 0.39 | -0.5 | 175 | -- |
| 165 | Cal Poly | BW | 15-14 | 0.9 | -0.01 | 6.62 | 0.7 | 163 | -- |
| 166 | UC Santa Barbara | BW | 15-13 | 0.9 | -0.14 | -2.20 | 2.2 | 146 | -- |
| 167 | Central Connecticut | NEC | 19-12 | 0.4 | -0.41 | -1.44 | -1.4 | 184 | -- |
| 168 | Boston University | AE | 20-13 | -0.6 | -0.45 | 5.67 | 0.1 | 169 | -- |
| 169 | Quinnipiac | NEC | 22-9 | -0.3 | -0.49 | 2.60 | -0.2 | 173 | -- |
| 170 | La Salle | A10 | 14-17 | -0.4 | -0.60 | 1.19 | -2.4 | 197 | -- |
| 171 | Stephen F. Austin | Slnd | 18-10 | -2.2 | -0.62 | -3.96 | -4.7 | 230 | -- |
| 172 | Middle Tennessee | SB | 16-15 | -0.8 | -0.77 | 3.36 | -4.8 | 232 | -- |
| 173 | Arkansas St. | SB | 17-15 | -3.3 | -0.80 | 2.44 | -2.0 | 191 | -- |
| 174 | Canisius | MAAC | 15-15 | -0.9 | -0.83 | -0.41 | -2.0 | 193 | -- |
| 175 | IUPU Fort Wayne | Sum | 18-12 | -1.7 | -0.92 | 1.57 | -0.8 | 179 | -- |
| 176 | Tulane | CUSA | 13-16 | -1 | -0.94 | -2.46 | -3.2 | 207 | -- |
| 177 | Massachusetts | A10 | 15-14 | -0.9 | -0.98 | -2.00 | 1.4 | 157 | -- |
| 178 | Texas Christian | MWC | 10-21 | -1.6 | -1.18 | -2.02 | -2.5 | 198 | -- |
| 179 | Loyola MD | MAAC | 15-15 | -1.7 | -1.38 | 1.43 | -2.2 | 194 | -- |
| 180 | Pennsylvania | Ivy | 13-14 | -1.1 | -1.58 | -0.01 | -0.6 | 176 | -- |
| 181 | Ball St. | MAC | 18-12 | -0.8 | -1.63 | -1.26 | -0.7 | 178 | -- |
| 182 | American | Pat | 22-9 | -1.9 | -1.74 | 1.17 | 3.3 | 133 | -- |
| 183 | Western Carolina | SC | 18-15 | -2.4 | -1.76 | -0.94 | 0.9 | 161 | -- |
| 184 | Tennessee Tech | OVC | 20-12 | -4.2 | -1.91 | 1.92 | -1.1 | 182 | -- |
| 185 | Jacksonville | ASun | 19-11 | -1.2 | -1.95 | -2.53 | 2.3 | 145 | -- |
| 186 | San Jose St. | WAC | 15-14 | -2.5 | -1.97 | 0.29 | 0.7 | 164 | -- |
| 187 | Evansville | MVC | 15-15 | -2.9 | -1.97 | -1.35 | 1.5 | 156 | -- |
| 188 | North Texas | SB | 21-10 | -2.5 | -2.06 | -3.28 | -0.1 | 171 | -- |
| 189 | Miami OH | MAC | 16-15 | -2.6 | -2.10 | 1.00 | 5.1 | 110 | 16 |
| 190 | Yale | Ivy | 15-13 | -2.8 | -2.36 | -1.44 | 0.2 | 168 | -- |
| 191 | Cornell | Ivy | 10-18 | -2.9 | -2.59 | 3.26 | -5.1 | 237 | -- |
| 192 | Charleston Southern | BSth | 16-16 | -5.5 | -2.70 | -1.23 | -4.1 | 226 | -- |
| 193 | Northeastern | CAA | 11-20 | -3 | -2.73 | 2.61 | -2.7 | 201 | -- |
| 194 | Florida Atlantic | SB | 21-10 | -2.4 | -2.81 | -3.89 | 4.8 | 115 | 16 |
| 195 | Sam Houston St. | Slnd | 17-12 | -1.5 | -2.82 | 3.90 | -0.3 | 174 | -- |
| 196 | Lehigh | Pat | 16-15 | -3.4 | -3.14 | -1.10 | -3.4 | 214 | -- |
| 197 | Virginia Military Inst | BSth | 18-13 | -3.9 | -3.32 | -0.18 | -2.4 | 196 | -- |
| 198 | Delaware | CAA | 14-17 | -3.4 | -3.35 | -0.17 | 0.8 | 162 | -- |
| 199 | Wyoming | MWC | 10-20 | -4 | -3.39 | 1.97 | -3.0 | 204 | -- |
| 200 | Mercer | ASun | 15-18 | -3.5 | -3.59 | 2.33 | -4.4 | 227 | -- |
| 201 | Bradley | MVC | 12-20 | -3.5 | -3.64 | 5.69 | -5.1 | 236 | -- |
| 202 | Maine | AE | 15-15 | -4.9 | -3.65 | -6.67 | -5.6 | 244 | -- |
| 203 | McNeese St. | Slnd | 19-10 | -4.2 | -3.66 | 1.88 | 0.5 | 167 | 17 |
| 204 | Houston | CUSA | 12-17 | -4.5 | -3.75 | -1.65 | -3.4 | 213 | -- |
| 205 | Auburn | SEC | 11-19 | -4.7 | -3.89 | 4.57 | -6.8 | 257 | -- |
| 206 | DePaul | BE | 7-23 | -3.7 | -3.93 | 1.13 | -3.3 | 211 | -- |
| 207 | Saint Joseph's | A10 | 9-21 | -4.6 | -4.04 | -0.39 | -2.3 | 195 | -- |
| 208 | Charlotte | A10 | 10-20 | -4.6 | -4.08 | -2.73 | -3.7 | 218 | -- |
| 209 | Loyola Marymount | WCC | 11-21 | -4 | -4.11 | -1.03 | -5.8 | 248 | -- |
| 210 | Eastern Kentucky | OVC | 15-16 | -7.2 | -4.22 | -2.15 | -6.1 | 254 | -- |
| 211 | Western Kentucky | SB | 16-15 | -4.9 | -4.28 | 0.32 | -3.3 | 210 | -- |
| 212 | Siena | MAAC | 13-18 | -4.9 | -4.43 | -3.67 | -3.7 | 219 | -- |
| 213 | Lamar | Slnd | 13-17 | -7.1 | -4.45 | -1.65 | -7.7 | 269 | -- |
| 214 | Nicholls St. | Slnd | 14-13 | -6.1 | -4.47 | -3.85 | -3.1 | 205 | -- |
| 215 | Savannah St. | ind | 11-18 | -10.9 | -4.50 | 3.92 | -2.5 | 200 | -- |
| 216 | St. Francis NY | NEC | 15-15 | -4.4 | -4.60 | 3.60 | -6.0 | 253 | -- |
| 217 | NC Wilmington | CAA | 13-18 | -5.1 | -4.74 | -1.20 | -3.2 | 209 | -- |
| 218 | William & Mary | CAA | 10-22 | -5.2 | -4.84 | 2.62 | -5.3 | 240 | -- |
| 219 | Drake | MVC | 13-18 | -5.4 | -4.94 | 2.45 | -4.1 | 224 | -- |
| 220 | UC Irvine | BW | 13-18 | -5.6 | -4.95 | -3.14 | -5.2 | 238 | -- |
| 221 | Denver | SB | 13-17 | -4.7 | -4.95 | -2.23 | -7.7 | 270 | -- |
| 222 | Arkansas Little Rock | SB | 17-16 | -6 | -5.07 | 0.10 | -3.5 | 215 | -- |
| 223 | Lafayette | Pat | 13-18 | -5.6 | -5.07 | 3.64 | -5.5 | 243 | -- |
| 224 | Cal St. Northridge | BW | 13-17 | -6.1 | -5.18 | 0.84 | -3.0 | 203 | -- |
| 225 | Appalachian St. | SC | 16-15 | -5.3 | -5.28 | 1.64 | -0.9 | 180 | -- |
| 226 | Georgia St. | CAA | 12-19 | -5.9 | -5.30 | -0.86 | -5.9 | 251 | -- |
| 227 | Utah Valley | GWC | 19-10 | -8.7 | -5.38 | -1.61 | -5.9 | 250 | -- |
| 228 | Stony Brook | AE | 15-16 | -5.3 | -5.39 | 1.81 | -7.3 | 265 | -- |
| 229 | Holy Cross | Pat | 8-21 | -5.9 | -5.48 | -1.61 | -11.5 | 307 | -- |
| 230 | Pepperdine | WCC | 12-21 | -6.2 | -5.80 | 1.98 | -3.1 | 206 | -- |
| 231 | Columbia | Ivy | 15-13 | -5.4 | -6.00 | -3.13 | -2.5 | 199 | -- |
| 232 | Louisiana St. | SEC | 11-20 | -6.2 | -6.08 | -0.30 | -6.0 | 252 | -- |
| 233 | Winthrop | BSth | 13-17 | -5.8 | -6.15 | 0.12 | -5.1 | 235 | -- |
| 234 | Southern Illinois | MVC | 13-19 | -6.8 | -6.16 | -2.29 | -3.8 | 220 | -- |
| 235 | Liberty | BSth | 19-13 | -7.1 | -6.20 | -3.26 | -1.5 | 188 | -- |
| 236 | Tennessee St. | OVC | 14-16 | -7 | -6.36 | -3.95 | -4.1 | 225 | -- |
| 237 | Elon | SC | 14-17 | -7.4 | -6.42 | -2.30 | -4.6 | 229 | -- |
| 238 | North Florida | ASun | 15-19 | -6.9 | -6.51 | -2.03 | 1.6 | 155 | -- |
| 239 | Louisiana Lafayette | SB | 14-15 | -6 | -6.54 | 4.06 | -5.4 | 241 | -- |
| 240 | Brown | Ivy | 11-17 | -7.8 | -6.69 | 1.32 | -7.0 | 262 | -- |
| 241 | Hampton | MEAC | 21-8 | -6.4 | -6.78 | -4.11 | -1.7 | 189 | 17 |
| 242 | UC Davis | BW | 10-20 | -7.5 | -6.81 | -2.03 | -7.5 | 268 | -- |
| 243 | Southeastern Louisiana | Slnd | 15-13 | -9.4 | -6.96 | 0.61 | -1.9 | 190 | -- |
| 244 | Wagner | NEC | 13-17 | -7.4 | -7.02 | -3.48 | -3.7 | 217 | -- |
| 245 | Albany | AE | 16-16 | -7.6 | -7.11 | -1.70 | -5.6 | 245 | -- |
| 246 | Cal St. Fullerton | BW | 11-19 | -8.9 | -7.36 | -0.51 | -7.0 | 263 | -- |
| 247 | Eastern Washington | BSky | 10-20 | -9.6 | -7.43 | 1.42 | -7.3 | 266 | -- |
| 248 | Illinois St. | MVC | 12-19 | -7.5 | -7.44 | -0.33 | -8.6 | 281 | -- |
| 249 | Louisiana Tech | WAC | 12-20 | -8.3 | -7.52 | -2.51 | -4.1 | 223 | -- |
| 250 | Texas San Antonio | Slnd | 16-13 | -6.9 | -7.57 | 1.89 | -3.9 | 222 | -- |
| 251 | Texas Arlington | Slnd | 13-16 | -8.6 | -7.74 | -4.15 | -6.4 | 255 | -- |
| 252 | Bowling Green | MAC | 13-18 | -8.7 | -7.97 | -3.01 | -5.1 | 234 | -- |
| 253 | Montana St. | BSky | 13-18 | -9.4 | -8.07 | -2.34 | -5.0 | 233 | -- |
| 254 | Wake Forest | ACC | 8-23 | -8.8 | -8.23 | -0.18 | -5.8 | 249 | -- |
| 255 | Illinois Chicago | Horz | 7-24 | -9.4 | -8.23 | 1.86 | -7.4 | 267 | -- |
| 256 | Youngstown St. | Horz | 9-21 | -9.1 | -8.27 | 1.12 | -6.9 | 259 | -- |
| 257 | Seattle | ind | 11-19 | -8.6 | -8.58 | 0.12 | -5.5 | 242 | -- |
| 258 | Texas St. | Slnd | 15-15 | -7.8 | -8.62 | 3.60 | -6.9 | 259 | -- |
| 259 | Presbyterian | BSth | 13-18 | -10.2 | -9.19 | -3.21 | -2.9 | 202 | -- |
| 260 | Campbell | ASun | 12-19 | -9.7 | -9.34 | -4.66 | -8.9 | 284 | -- |
| 261 | UC Riverside | BW | 11-18 | -11.7 | -9.45 | -0.55 | -4.6 | 228 | -- |
| 262 | Chattanooga | SC | 16-16 | -12.1 | -9.50 | -0.25 | -2.0 | 192 | -- |
| 263 | Sacred Heart | NEC | 11-18 | -10.6 | -9.61 | 0.44 | -9.8 | 295 | -- |
| 264 | Mount St. Mary's | NEC | 11-21 | -10.4 | -9.76 | -0.27 | -6.9 | 261 | -- |
| 265 | Northern Illinois | MAC | 9-20 | -10.5 | -9.79 | -2.97 | -9.9 | 297 | -- |
| 266 | Morgan St. | MEAC | 15-13 | -9.4 | -9.84 | -1.61 | -6.8 | 258 | -- |
| 267 | Gardner Webb | BSth | 11-21 | -10.6 | -9.89 | 2.24 | -5.7 | 247 | -- |
| 268 | Coppin St. | MEAC | 16-13 | -8.9 | -9.97 | 1.54 | -5.7 | 246 | -- |
| 269 | Southern Utah | Sum | 11-19 | -8.8 | -9.97 | 3.94 | -9.3 | 291 | -- |
| 270 | Jackson St. | SWAC | 16-14 | -12.3 | -10.05 | -4.43 | -8.5 | 280 | -- |
| 271 | Troy | SB | 8-21 | -11.5 | -10.30 | -1.20 | -8.9 | 283 | -- |
| 272 | Navy | Pat | 11-20 | -10.4 | -10.38 | 1.90 | -10.0 | 298 | -- |
| 273 | Northwestern St. | Slnd | 18-13 | -10.1 | -10.56 | 0.85 | -4.8 | 231 | -- |
| 274 | Portland St. | BSky | 13-16 | -12.5 | -10.95 | -4.14 | -7.9 | 271 | -- |
| 275 | Southeast Missouri St. | OVC | 10-22 | -13.3 | -10.96 | 4.57 | -11.0 | 303 | -- |
| 276 | Towson | CAA | 4-26 | -11.6 | -10.99 | -0.68 | -13.6 | 323 | -- |
| 277 | Florida Gulf Coast | ASun | 10-20 | -11.5 | -11.20 | 4.05 | -9.2 | 288 | -- |
| 278 | Missouri Kansas City | Sum | 16-14 | -11.8 | -11.20 | -1.36 | -3.5 | 216 | -- |
| 279 | South Dakota | GWC | 16-14 | -13.8 | -11.29 | -2.81 | -11.1 | 304 | -- |
| 280 | South Alabama | SB | 12-16 | -13.7 | -11.34 | -0.54 | -8.1 | 274 | -- |
| 281 | Jacksonville St. | OVC | 5-25 | -11.9 | -11.36 | 3.55 | -16.2 | 334 | -- |
| 282 | Eastern Michigan | MAC | 9-21 | -11.4 | -11.41 | 0.30 | -11.8 | 312 | -- |
| 283 | Central Michigan | MAC | 10-20 | -11.6 | -11.44 | 0.33 | -9.2 | 288 | -- |
| 284 | Monmouth | NEC | 9-21 | -12.1 | -11.48 | 1.86 | -12.6 | 317 | -- |
| 285 | NC Greensboro | SC | 7-24 | -12.2 | -11.50 | 1.28 | -11.3 | 306 | -- |
| 286 | Texas Southern | SWAC | 18-11 | -12 | -11.71 | -3.88 | -3.2 | 208 | 17 |
| 287 | St. Francis PA | NEC | 9-21 | -12.5 | -11.87 | -1.10 | -9.1 | 287 | -- |
| 288 | New Hampshire | AE | 12-18 | -12.9 | -11.88 | -1.58 | -9.1 | 286 | -- |
| 289 | Army | Pat | 11-19 | -12.7 | -11.94 | -5.72 | -9.6 | 293 | -- |
| 290 | North Carolina A&T | MEAC | 15-16 | -13.3 | -11.94 | 0.60 | -5.2 | 239 | -- |
| 291 | Bethune Cookman | MEAC | 20-11 | -13.8 | -12.14 | 2.13 | -3.4 | 212 | -- |
| 292 | Florida International | SB | 11-19 | -12.9 | -12.23 | -0.73 | -10.4 | 300 | -- |
| 293 | San Diego | WCC | 6-24 | -14 | -12.43 | 0.82 | -8.4 | 278 | -- |
| 294 | The Citadel | SC | 10-22 | -12.6 | -12.47 | -4.33 | -9.3 | 290 | -- |
| 295 | Tennessee Martin | OVC | 12-21 | -14 | -12.71 | 0.39 | -8.4 | 279 | -- |
| 296 | Eastern Illinois | OVC | 9-20 | -14.4 | -12.84 | -4.83 | -11.2 | 305 | -- |
| 297 | Hartford | AE | 11-20 | -14 | -12.93 | -2.58 | -11.0 | 302 | -- |
| 298 | Fordham | A10 | 7-21 | -13.3 | -13.03 | -0.81 | -9.5 | 292 | -- |
| 299 | NJ Inst of Technology | GWC | 15-14 | -15.2 | -13.10 | 2.34 | -10.5 | 301 | -- |
| 300 | Norfolk St. | MEAC | 10-19 | -14.4 | -13.11 | -2.14 | -12.0 | 313 | -- |
| 301 | North Dakota | GWC | 16-14 | -14.6 | -13.13 | 0.25 | -8.2 | 276 | -- |
| 302 | Niagara | MAAC | 9-23 | -14.3 | -13.18 | 1.18 | -9.8 | 294 | -- |
| 303 | Delaware St. | MEAC | 9-20 | -16.5 | -13.78 | -6.49 | -10.3 | 299 | -- |
| 304 | Manhattan | MAAC | 6-25 | -15.3 | -14.08 | 1.39 | -12.4 | 316 | -- |
| 305 | North Carolina Central | ind | 15-14 | -15.9 | -14.28 | -2.08 | -6.8 | 256 | -- |
| 306 | Stetson | ASun | 8-23 | -14.9 | -14.29 | 0.97 | -11.7 | 311 | -- |
| 307 | Idaho St. | BSky | 9-20 | -15.3 | -14.75 | -1.95 | -8.2 | 277 | -- |
| 308 | Bryant | NEC | 9-21 | -17 | -14.80 | -3.75 | -9.0 | 285 | -- |
| 309 | Longwood | ind | 12-19 | -20.2 | -14.99 | 3.57 | -7.3 | 264 | -- |
| 310 | Mississippi Valley St. | SWAC | 13-18 | -16.8 | -15.24 | -2.50 | -7.9 | 272 | -- |
| 311 | High Point | BSth | 12-19 | -17 | -15.60 | -0.24 | -7.9 | 273 | -- |
| 312 | Alabama St. | SWAC | 14-17 | -16.8 | -16.12 | 6.96 | -11.7 | 308 | -- |
| 313 | Marist | MAAC | 6-27 | -17.8 | -16.20 | 1.80 | -11.7 | 309 | -- |
| 314 | Texas A&M Corpus Chris | Slnd | 10-21 | -17.4 | -16.52 | -0.82 | -8.1 | 275 | -- |
| 315 | Binghamton | AE | 8-23 | -17.9 | -16.67 | 4.63 | -14.0 | 325 | -- |
| 316 | Fairleigh Dickinson | NEC | 5-24 | -17.8 | -16.81 | -2.85 | -17.4 | 338 | -- |
| 317 | South Carolina Upstate | ASun | 5-25 | -18.5 | -17.05 | -3.05 | -11.7 | 310 | -- |
| 318 | Samford | SC | 12-19 | -17.5 | -17.14 | -2.70 | -8.6 | 282 | -- |
| 319 | Colgate | Pat | 7-23 | -18.5 | -17.16 | 1.70 | -13.0 | 319 | -- |
| 320 | Cal St. Bakersfield | ind | 9-19 | -18.7 | -17.25 | -8.81 | -9.9 | 296 | -- |
| 321 | Sacramento St. | BSky | 7-21 | -18.8 | -17.36 | -0.05 | -13.2 | 321 | -- |
| 322 | Alabama A&M | SWAC | 13-14 | -16.8 | -17.50 | 0.01 | -13.7 | 324 | -- |
| 323 | Kennesaw St. | ASun | 8-23 | -19.6 | -17.78 | 1.92 | -12.1 | 314 | -- |
| 324 | Dartmouth | Ivy | 5-23 | -19.2 | -18.29 | -3.55 | -13.0 | 320 | -- |
| 325 | South Carolina St. | MEAC | 9-21 | -20.6 | -18.77 | 2.11 | -17.2 | 337 | -- |
| 326 | Florida A&M | MEAC | 12-19 | -20.1 | -18.79 | -0.60 | -12.6 | 318 | -- |
| 327 | Western Illinois | Sum | 7-23 | -21.7 | -19.75 | -2.55 | -14.4 | 326 | -- |
| 328 | Grambling | SWAC | 10-20 | -21.4 | -19.88 | 5.75 | -15.9 | 333 | -- |
| 329 | Georgia Southern | SC | 5-27 | -20.1 | -19.88 | 1.27 | -16.6 | 336 | -- |
| 330 | Louisiana Monroe | SB | 7-24 | -21.6 | -19.98 | -1.98 | -14.4 | 327 | -- |
| 331 | Radford | BSth | 5-24 | -21.3 | -20.23 | -0.46 | -13.5 | 322 | -- |
| 332 | Central Arkansas | Slnd | 5-24 | -24.4 | -20.29 | -3.85 | -17.9 | 339 | -- |
| 333 | Prairie View A&M | SWAC | 10-21 | -23.9 | -20.69 | -0.51 | -14.7 | 328 | -- |
| 334 | Toledo | MAC | 4-27 | -24.2 | -20.80 | -3.68 | -15.8 | 332 | -- |
| 335 | Texas Pan American | GWC | 6-24 | -23.8 | -22.08 | -2.26 | -18.9 | 341 | -- |
| 336 | Maryland Eastern Shore | MEAC | 8-21 | -24.5 | -22.63 | 0.96 | -14.9 | 330 | -- |
| 337 | Arkansas Pine Bluff | SWAC | 7-23 | -26 | -23.44 | -3.18 | -15.4 | 331 | -- |
| 338 | MD Baltimore County | AE | 5-25 | -25.9 | -23.97 | -2.32 | -16.3 | 335 | -- |
| 339 | Howard | MEAC | 6-23 | -25.3 | -23.99 | 0.81 | -20.2 | 343 | -- |
| 340 | SIU Edwardsville | ind | 8-21 | -29.7 | -24.10 | 0.09 | -12.4 | 315 | -- |
| 341 | Houston Baptist | GWC | 4-25 | -25.1 | -24.20 | -1.12 | -23.9 | 344 | -- |
| 342 | Alcorn St. | SWAC | 4-24 | -27.7 | -25.04 | -0.15 | -19.6 | 342 | -- |
| 343 | Centenary | Sum | 1-29 | -31.1 | -30.62 | 2.78 | -18.6 | 340 | -- |
| 344 | Southern | SWAC | 4-26 | -34.7 | -33.63 | -4.08 | -25.2 | 345 | -- |
| 345 | Chicago St. | GWC | 6-25 | -36.7 | -33.86 | -2.98 | -14.9 | 329 | -- |